Introduction to Spatial Audio

The Spatial Dimension in Natural Sound

Width: left ↔ right placement of sounds
Height: perception of vertical position
Depth: distance and front-to-back layering

Natural Sound in Outdoor Environments

Multiple sound sources with unique locations and qualities
Natural blending creates a diffuse soundscape
Contrast between background ambience and identifiable events

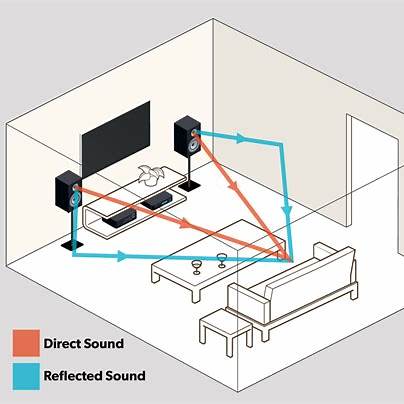
Natural Sound in Indoor Environments

Reflections shape how sound is perceived
Reflections reveal size and character of the space
Contrast between direct and reflected sound is key

Guess the Environment?

Sound Intensity in a Free Field

The key concept is the inverse-square law: as sound radiates outward from a source, its intensity decreases with the square of the distance.

Omnidirectional Radiation

Imagine a sound source that radiates equally in every direction—what we call an omnidirectional source.

The sound energy spreads out spherically, like ripples on a pond, but in 3D.
The power of the source is represented as W (watts).
As this energy moves outward, it must cover more and more surface area.

Ask students: If the same amount of power is spread over a larger area, what happens to the intensity?

Surface Area and Intensity

The surface area of a sphere increases as we move farther away from the source:

Formula: S = 4πr².
Intensity is defined as Power ÷ Area, so: I = W / (4πr²).

This means intensity doesn’t decrease linearly with distance—it decreases much faster, with the square of distance.

Analogy: Think about butter spread over bread. If the bread is small, the butter layer is thick. If the bread is twice as large, the same butter covers it more thinly. The “flavor” (intensity) weakens.

Doubling Distance Effect

Now, here’s the important rule of thumb:

At distance r, a patch of energy covers 1 m².
At distance 2r, that same energy must now cover 4 m².
So, intensity is reduced to one-quarter.

In sound terms, this is about a 6 dB drop every time you double the distance.

Ask students: If we start at 1 meter from the source, how many dB lower will it sound at 4 meters? (Answer: 12 dB lower, since doubling twice = two 6 dB drops.)

Visual Explanation of the Diagrams

(a) Spherical Model

A sphere radiates outward from the source.
Energy that passes through a 1 m² patch at distance r spreads thinner as the sphere expands.

(b) Expansion Model

The cube-like sketch shows how a fixed energy beam expands from 1 m² at r to 4 m² at 2r.
It illustrates the same inverse-square relationship in a more geometric way.

Key Takeaways

Sound intensity decreases with the inverse-square of distance.
Doubling distance reduces intensity to one-quarter.
In decibels, every doubling of distance equals a 6 dB drop.
This principle is essential in live sound, recording, and acoustic design.

Final question for students: How might this principle affect microphone placement in a concert recording?

Answer

When placing microphones for a concert, the inverse-square law means that distance has a dramatic effect on the captured level:

Closer placement: If the microphone is close to the source, the captured sound will be much louder and more direct. This reduces the influence of room acoustics and ambient noise. That’s why close-miking is common for individual instruments.
Further placement: As you move the microphone farther away, intensity drops quickly. For every doubling of distance, the level decreases by 6 dB. This means distant microphones require more gain, which can also bring up background noise.
Balance of direct vs. ambient sound: Engineers often combine close mics (for clarity) with distant or overhead mics (to capture the natural reverb and ensemble blend). The inverse-square law helps explain why the distant mics sound quieter and more diffuse—they’re catching less direct energy and more reflections.
Practical implication: If you double the mic’s distance from a violinist—from 1 m to 2 m—you don’t just lose a little volume, you lose a quarter of the intensity. That affects both loudness balance and the clarity of the recording.

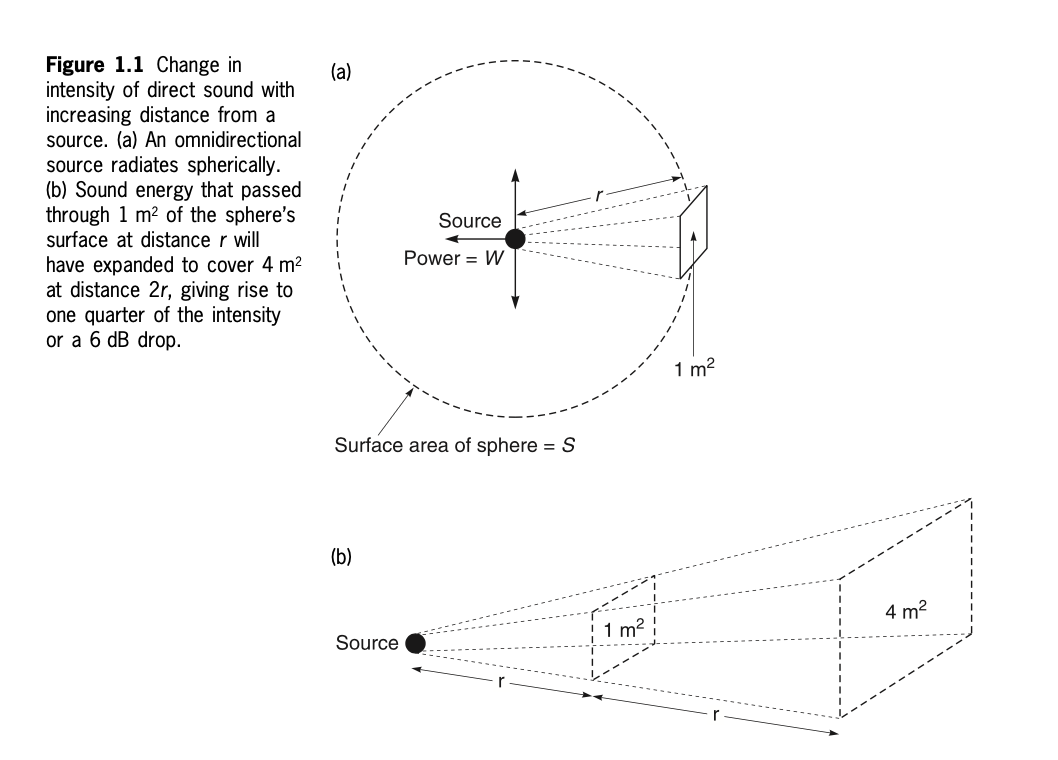
Sound Directivity

Directivity Patterns of Sound Sources

Diagram shows how much energy a source radiates at different angles.
Radiation is not uniform: more energy is radiated to the front (0° axis).
Directivity increases with frequency.

Key Observations

LF (Low Frequency, solid line)
- Radiation pattern is broader and more rounded.
- Energy spreads more evenly around the source.
- Less directional.
HF (High Frequency, dash-dot line)
- Pattern is narrower and elongated forward.
- Strong emphasis on the 0° axis.
- Much less energy radiated to the sides (90°/270°) or back (180°).
- More directional.

Acoustic Meaning

At low frequencies, sound wraps around obstacles and radiates almost omnidirectionally.
At high frequencies, sound beams forward, creating a focused projection.
This is why bass feels “everywhere” in a room, but treble seems more localized.

Applications

Microphone pickup patterns work on the same principle (e.g., cardioid polar plots).
Loudspeaker design uses directivity to control coverage in a venue.
In recording and live sound, understanding directivity helps with mic placement, avoiding bleed, and controlling reflections.

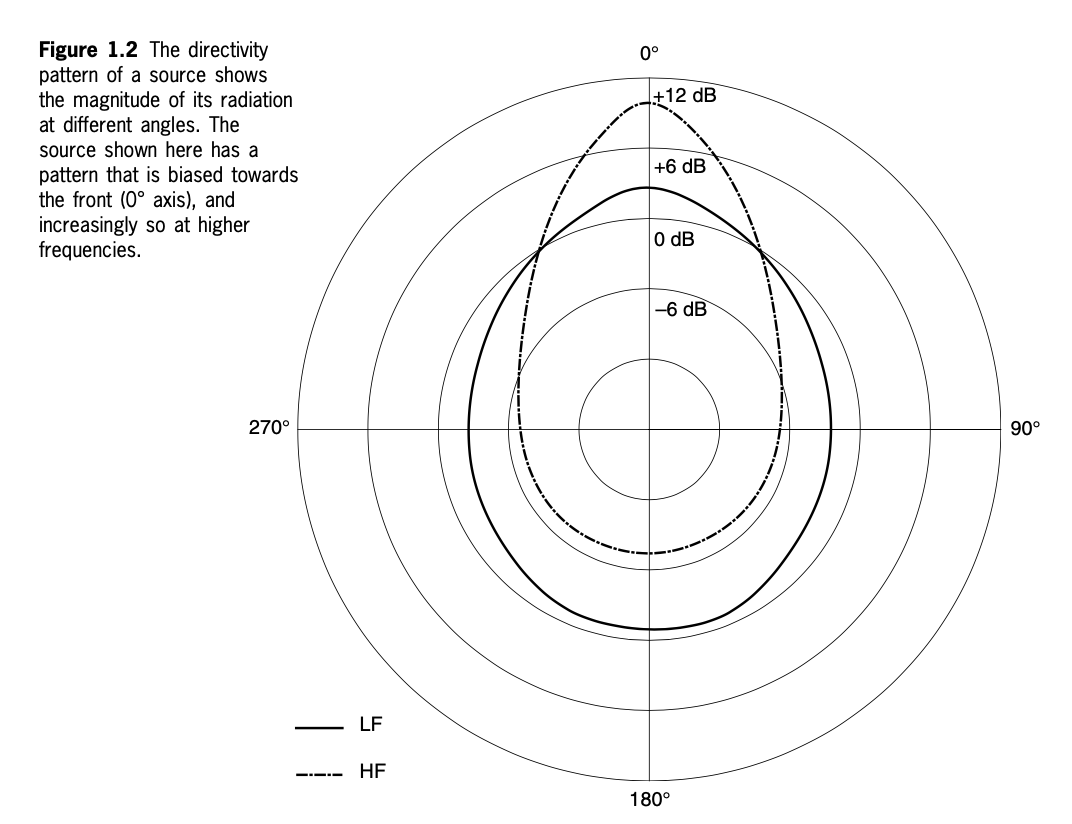
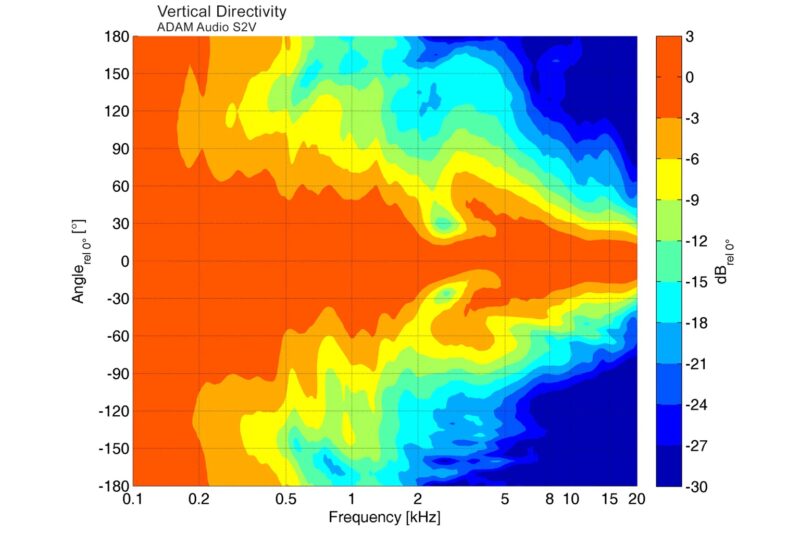
Real-World Examples of Directivity Patterns

Adam Audio Speaker Directivity Chart

What the plot shows

X-axis: frequency (kHz), ~0.1–20 on a log scale.
Y-axis: vertical angle relative to the tweeter axis (0°), from −180° to +180°.
Color: level in dB relative to 0° (warm colors ≈ louder; cool colors ≈ attenuated).

How to read it

Low frequencies (≤ ~300–500 Hz): wide “orange” band across many angles → near-omnidirectional vertically.
Midband (~1–3 kHz): pattern begins to pinch; alternating yellow/green bands indicate vertical lobing around the crossover region.
High frequencies (≥ ~5–10 kHz): narrow orange core centered at 0° with rapid falloff to green/blue → small vertical sweet spot.

Approximate landmarks (read from color transitions)

Around 1 kHz: useful coverage to roughly ±60° before substantial roll-off.
Around 5 kHz: useful coverage tightens to roughly ±30°.
≥10 kHz: useful coverage can be as tight as ±15–20° (levels drop quickly away from 0°).

Why it matters

Ear height: align ears close to the tweeter’s 0° axis to keep HF balance.
Tilt: angle monitors so the 0° axis meets the listener’s ears; small up/down moves can change brightness.
Reflections: desk and ceiling paths are typically off-axis vertically; their HF content is reduced relative to direct sound, but midband lobing can color those reflections.
Placement decisions: for multiple listeners or standing positions, consider stands/tilt to keep everyone within the HF coverage; for a single mix position, aim precisely at ear height.
Design angle: waveguides/horns and coaxial drivers are used to control or stabilize this pattern, trading width for consistency.

Prompt for discussion

If a listener stands up 20–30 cm, which frequency range changes most audibly, and why?
How would you adjust speaker tilt or seat height to keep the spectral balance stable across sessions?

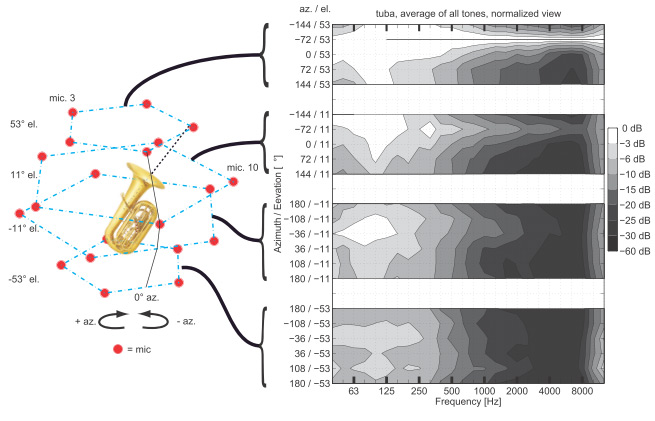
Real-World Example: Tuba Directivity

Reading the figure

Left: measurement array of microphones around the tuba at four elevation rings (about +53°, +11°, −11°, −53°).
Right: four heatmaps (one per elevation).
- X-axis: frequency (≈63 Hz to 8 kHz).
- Y-axis: azimuth angle at that elevation (−180° to +180°, front at 0°).
- Color/gray scale: level relative to the on-axis reference (0 dB = loudest), down to about −60 dB.
The plot is normalized, so it shows relative level vs. direction rather than absolute SPL.

What it shows

63–250 Hz: broad, near-omnidirectional radiation at all angles; the instrument body radiates, so bell aim matters less.
500 Hz–2 kHz: pattern begins to concentrate toward the bell; side and rear levels fall by ~10–20 dB depending on elevation.
2–4 kHz: strong beaming along the bell axis (forward and slightly upward), with steep roll-off to the sides and rear (often >20–30 dB down).
Elevation asymmetry: upper rings show more HF energy than lower rings, consistent with the bell pointing upward/forward.

Practical implications

Mic placement for clarity/brightness: aim near the bell axis (slightly above and in front) to capture mid/high partials and articulation.
Warmer, rounder tone: move off-axis toward the side of the bell or lower elevation to reduce HF beaming and key/valve noise.
Section balance and seating: players and listeners above/forward of the bell hear more definition; those off to the side/rear perceive less brightness.
Live sound: a single overhead or front-of-bell mic will translate articulation; add a side or room mic to recover body and low-end bloom.
Recording consistency: mark bell aim and mic height—small vertical changes can shift HF capture noticeably.

Prompts for discussion

If you want more articulation without boosting EQ, which direction should you move the mic, and why?
How might this pattern inform the placement of baffles or reflectors in a live hall to improve clarity without making the sound harsh?

Sources in Reflective Spaces

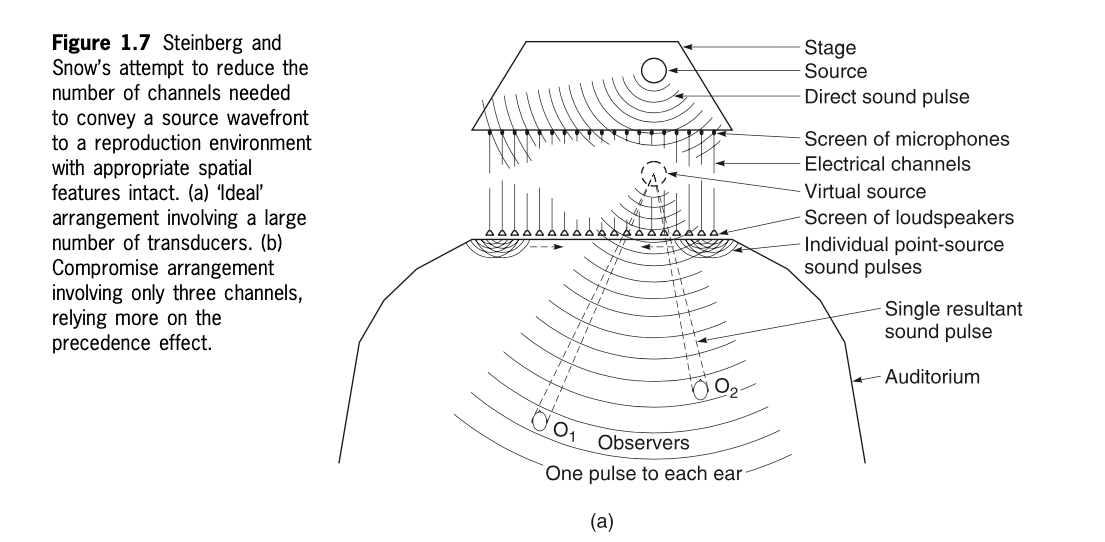
Introduction to Spatial Reproduction of Sound

Two aims: recreate real acoustic spaces or design imagined spaces
Three approaches: channel-based (stereo, 5.1), object-based (e.g., Atmos), scene-based (Ambisonics/HOA)
Two delivery modes: loudspeakers (room-interactive) and headphones/binaural (HRTF-based)

Overview

Recreate natural environments: capture or model real spaces (e.g., concert hall impulse responses, Decca Tree, or 5.1 per ITU-R BS.775). The goal is plausibility and fidelity to the original venue. ([ITU][1], [AES][2])
Create virtual environments: place and move sounds anywhere in 3D, independent of an original space (film, games, XR).

Core paradigms

Channel-based: fixed speaker feeds; phantom imaging between loudspeakers. ITU-R BS.775 defines reference angles for 5.1 layouts used in production/playback. ([ITU][1], [AES][2])
Object-based: each element carries position metadata; a renderer adapts playback to any certified layout (e.g., Atmos). ([professional.dolby.com][3], [Audient][4])
Scene-based (Ambisonics/HOA): encode the sound field with spherical harmonics; decode to speakers or to binaural. ([Microsoft][5], [Wikipedia][6])

Delivery and perception

Loudspeakers: listener hears direct sound plus room interactions; layout and room treatment shape localization, envelopment, and timbre. ITU reference layouts provide a consistent baseline. ([ITU][1])
Headphones/binaural: HRTFs and head-tracking maintain externalization and stable localization as the head moves. ([MathWorks][7], [MDPI][8])

Evaluation criteria (use when comparing systems in class)

Localization accuracy and stability with listener movement
Externalization vs. “in-head” sensation
Envelopment and spatial resolution
Spectral fidelity (no excessive coloration)

Teaching prompts

When would you choose object-based over channel-based for a touring show?
How does head-tracking improve externalization in VR compared to static binaural?

Early Sound Reproducing Equipment

The Théâtrophone: An Early Stereo Transmission

Théâtrophone Poster by Jules Chéret

Bell Labs in the 1930s

Speaker Notes

This diagram shows an early experiment in spatial sound reproduction by Steinberg and Snow at Bell Labs in the 1930s.
Their question: How many channels are needed to reproduce the spatial impression of a real source on stage for an audience?

Step 1: The “Ideal” Concept

Imagine a screen of microphones in front of the stage, each capturing the wavefront at a slightly different position.
Each mic feeds a matching loudspeaker screen in the auditorium.
Together, the loudspeakers recreate the original sound wavefront—so every listener perceives the correct direction and timing, no matter where they sit.
In theory, this is perfect wavefield reproduction, but it requires a huge number of transducers.

Step 2: The Compromise

Steinberg & Snow realized you could get most of the effect with far fewer channels.
By using just three channels (Left–Center–Right), you can still create a stable sound image for a wide audience.
This works because of the precedence effect: our ears lock onto the first-arriving sound to determine direction. Later arrivals reinforce loudness without shifting localization.

Why It Matters

Their work laid the foundation for cinema LCR playback systems, later evolving into stereo and surround.
It also framed two continuing approaches in spatial audio:
1. Wavefront reconstruction (many sources, physical accuracy).
2. Psychoacoustic rendering (few sources, exploiting how humans localize).

Teaching Prompt

You might ask students: Why does the center channel help stabilize the image compared to stereo?
Or demonstrate with clicks through two vs. three speakers—listeners off to the side will notice the center channel keeps the image anchored.

Binaural Recording

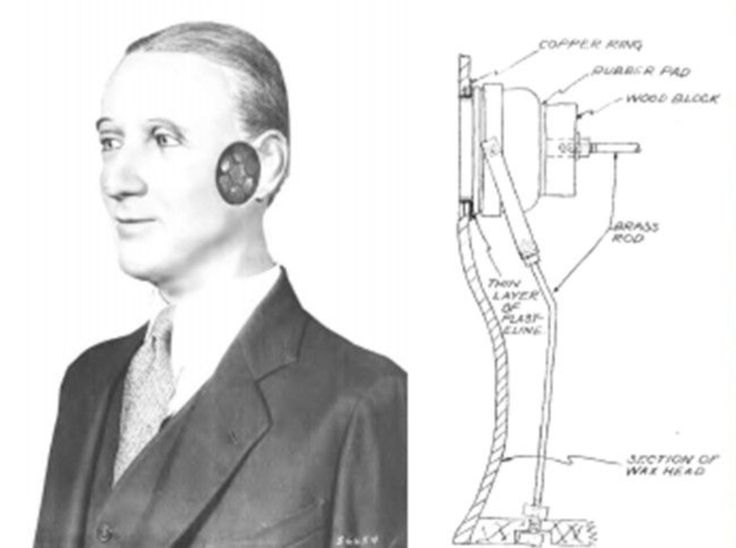
Binaural Head Diagram

What is Binaural Recording?
- Binaural stereo aims to recreate the experience of listening with two human ears.
- Uses microphones positioned at ear-level to simulate natural human hearing.
- When reproduced through headphones, binaural recordings create a highly realistic spatial experience.
Diagram Explanation:
- Left Side: Early model of a binaural head used for binaural recordings, designed to simulate how humans perceive sound directionally.
- Right Side: Cross-section showing internal components:
  - Copper Ring, Rubber Pad, Wood Block: Elements that simulate the density and sound-blocking characteristics of the human head.
  - Brass Rod and Thin Layer of Plastic: Components that mimic sound transmission through the human ear.
  - Wax Head: Designed to replicate the acoustic properties of a real human head and ears, providing realistic spatial audio cues.
Key Concepts:
- Binaural recordings rely on the subtle timing and amplitude differences between the two “ears” to recreate spatial realism.
- When played back through headphones, they provide a sense of directionality—front, back, above, below—similar to natural hearing.
- This method is especially effective in applications such as virtual reality (VR), gaming, and immersive audio.

Historical Background:

Who Made It?: This particular binaural head was pioneered by Harvey Fletcher and Bell Laboratories in the 1930s.
When?: The concept of binaural recording dates back to the late 19th century, but modern implementations, like this one, became more prominent in the 1930s. Fletcher’s work at Bell Labs greatly contributed to advancing this technique, allowing for the development of immersive 3D sound experiences.

Ambisonics

Developed in the 1970s
360° Sound Field (Including height)
Key Contributors: Peter Fellgett & Michael Gerzon
Applications: Virtual reality, immersive audio

For more, visit: History of Ambisonics

The Home Cinema and ITU-Standard Surround Sound

Applications of Spatial Audio

Military Communication: Enhances situational awareness in combat by spatializing voices, reducing cognitive overload.
Example: Spatial Audio in Tactical Communication
Teleconferencing: Improves clarity and reduces fatigue in multi-participant remote meetings by spatializing voices.
Example: Spatial Audio in Remote Conferencing
Education: Enhances learning experiences through spatial audio in immersive virtual environments.
Example: Spatial Audio for Education
Therapy and Stress Reduction: Used to reduce stress and anxiety in clinical and non-clinical populations.
Example: Spatial Audio for Stress Reduction